Local Quantum Mechanical Prediction of the Singlet State Using Geometric Algebra
Author
Fred Diether
Title
Local Quantum Mechanical Prediction of the Singlet State Using Geometric Algebra
Description
Local Quantum Mechanical Prediction of the Singlet State
Category
Academic Articles & Supplements
Keywords
Local Quantum Mechanical Prediction, Singlet State, Geometric Algebra
URL
http://www.notebookarchive.org/2025-08-cy1qgme/
DOI
https://notebookarchive.org/2025-08-cy1qgme
Date Added
2025-08-28
Date Last Modified
2025-08-28
File Size
0.76 megabytes
Supplements
Rights
CC BY 4.0

Supplemental Material for Carl Diether, “Local Quantum Mechanical Prediction of the
Singlet State using Geometric Algebra”
Validation of the Local QM Product Calculation Prediction Using Pauli Matrices
and Geometric Algebra with 3D Vectors, Based on Joy Christian’s 3-Sphere Model.
Singlet State using Geometric Algebra”
Validation of the Local QM Product Calculation Prediction Using Pauli Matrices
and Geometric Algebra with 3D Vectors, Based on Joy Christian’s 3-Sphere Model.
Local Quantum Mechanical Prediction of the Singlet State Using Geometric AlgebraCreated by Carl Diether Aug. 2025
Load Clifford Package, Set Run Time Parameters, Initialize Arrays and Table
In[]:=
<<"clifford.m"m=30000;s1=ConstantArray[0,m];s2=ConstantArray[0,m];σs1=ConstantArray[0,m];σs2=ConstantArray[0,m];a1=ConstantArray[0,m];b1=ConstantArray[0,m];gA=ConstantArray[0,m];gB=ConstantArray[0,m];A=ConstantArray[0,m];B=ConstantArray[0,m];pc=ConstantArray[0,m];plotpc=Table[{0,0},m];I3=Pseudoscalar[3];
Generating Particle Data with Three Independent Do-Loops
In[]:=
Do[s=RandomPoint[Sphere[]];(*UniformUnit3DVectors*)s1[[h]]=s;(*SpinvectortoA*)s2[[h]]=-s;(*SpinvectortoB*)σs1[[h]]=PauliMatrix[1]*s[[1]]+PauliMatrix[2]*s[[2]]+PauliMatrix[3]*s[[3]];(*ParticlespintoA*)σs2[[h]]=-(PauliMatrix[1]*s[[1]]+PauliMatrix[2]*s[[2]]+PauliMatrix[3]*s[[3]]),{h,m}](*ParticlespintoB*)
Doa=RandomPoint[Sphere[]];(*UniformUnit3DVectors*)a1[[h]]=a;σa=PauliMatrix[1]*a[[1]]+PauliMatrix[2]*a[[2]]+PauliMatrix[3]*a[[3]];(*Detectionpolarizer*)cosas1=ReFullSimplifyExtractFlatten(
).σa.σs1[[h]].
+(
).σa.σs1[[h]].
,1+i;(*Particle-Detectorinteraction*)ra=Cross[a,s1[[h]]].{e[1],e[2],e[3]};(*Vectorcrossproduct*)rc=InnerProduct[I3,ra];(*Converttobivector*)gA[[h]]=cosas1+rc;(*Converttomultivector*)A[[h]]=Sign[a.s1[[h]]],{h,m}
1
2
1 | 0 |
1 |
0 |
0 | 1 |
0 |
1 |
Dob=RandomPoint[Sphere[]];(*UniformUnit3DVectors*)b1[[h]]=b;σb=PauliMatrix[1]*b[[1]]+PauliMatrix[2]*b[[2]]+PauliMatrix[3]*b[[3]];(*Detectionpolarizer*)cosbs2=ReFullSimplifyExtractFlatten(
).σs2[[h]].σb.
+(
).σs2[[h]].σb.
,1+i;(*Particle-Detectorinteraction*)rb=Cross[s2[[h]],b].{e[1],e[2],e[3]};(*Vectorcrossproducts*)rd=InnerProduct[I3,rb];(*Converttobivector*)gB[[h]]=cosbs2+rd;(*Converttomultivector*)B[[h]]=Sign[b.s2[[h]]],{h,m}
1
2
1 | 0 |
1 |
0 |
0 | 1 |
0 |
1 |
Verification of the Local QM Product Calculation Prediction
In[]:=
Do[r0=Expand[({e[1],e[2],e[3]}).(Re[gA[[h]]]*Limit[Cross[s4,b1[[h]]],s4Sign[Re[gB[[h]]]]b1[[h]]]+Re[gB[[h]]]*Limit[Cross[a1[[h]],s3],s3Sign[Re[gA[[h]]]]a1[[h]]]-Cross[Limit[Cross[a1[[h]],s3],s3Sign[Re[gA[[h]]]]a1[[h]]],Limit[Cross[s4,b1[[h]]],s4Sign[Re[gB[[h]]]]b1[[h]]]])];Lr0=InnerProduct[I3,r0];qpc=Re[GeometricProduct[gA[[h]],gB[[h]]]]+Lr0;(*ProductCalculation*)pc[[h]]=qpc;ϕa=ArcTan[a1[[h]][[1]],a1[[h]][[2]]];ϕb=ArcTan[b1[[h]][[2]],b1[[h]][[1]]];If[ϕa*ϕb>0,angle=ArcCos[a1[[h]].b1[[h]]]/Degree,angle=(2π-ArcCos[a1[[h]].b1[[h]]])/Degree];plotpc[[h]]={angle,qpc},{h,m}]
In[]:=
simulation=ListPlot[plotpc,PlotMarkers{Automatic,Small},AspectRatio9/16,Ticks{{{90,90°},{180,180°},{0,0°},{270,270°},{360,360°}},Automatic},GridLinesAutomatic,AxesOrigin{0,-1.0}];negcos=Plot[-Cos[xDegree],{x,0,360},PlotStyle{Magenta}];p1=Plot[-1+2x1Degree/π,{x1,0,180},PlotStyle{Gray,Dashed}];p2=Plot[3-2x2Degree/π,{x2,180,360},PlotStyle{Gray,Dashed}];Show[simulation,p1,p2,negcos]
Out[]=
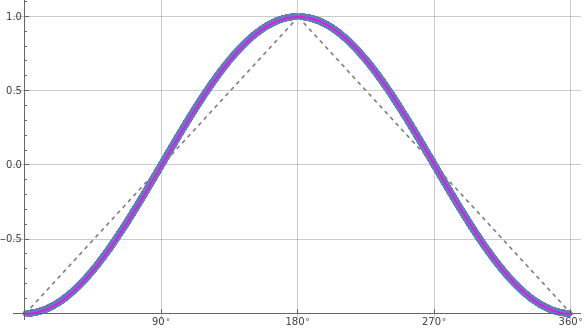
Blue is the correlation data, magenta is the negative cosine curve for an exact match.
Computing Averages
In[]:=
AveA=N[Total[A]/m];AveB=N[Total[B]/m];Print[" <A> = ",AveA," <B> = ",AveB];meanpc=Expand[Mean[pc]];Print["Cross products vanish, meanpc = ",meanpc];
<A> = 0.0074 <B> = -0.0018
Cross products vanish, meanpc = -0.00260275
Cite this as: Fred Diether, "Local Quantum Mechanical Prediction of the Singlet State Using Geometric Algebra" from the Notebook Archive (2025), https://notebookarchive.org/2025-08-cy1qgme
Download
